Posts by Miwarre

Oh well, it is always surprising how different peoples see things with different perspective. To me furnace loading is already too simple and "quick-and-dirty"!

For instance, you can put and remove ores while the furnace is burning, and there is no cool down time (which in the reality lasts for hours and sometimes for days); also, the smelting time seems too short, but I have no solid figures on that.

There is also to consider if timing should be compared to a fixed scaling of the real time or to the time rate set in the simulation. IIUC, currently, operations last a fixed amount regardless of the simulation time rate; this applies to many things: smelting time, vegetation growth, hunger/thirst increase, etc.

@yahgiggle: in addition, the example [II] in the OP seems to implies that the current implementation suffers from gimbal lock, which isn't a good thing and might imply that, no, not all orientations can be achieved.

Thanks for the encouragement, @yahgiggle! Still, if you know a way to achieve this result and would like to share, I would be very grateful!

@botchikii: Thanks to you for the great addition: les francophones vont être heureux!

I am also glad that my decision to externalise the texts to ease translation is finding some use!

Quote from ArcticuKitsu

Flag Marker: One flag to the next would give you the number you're seeking.
[...]
Some for short distances, some for longer distances.

Medium-to-long distance measurement is already available in my GPS plugin: it is possible to define up to 9 waypoints and to have the distance of each from the current player position.

Not exactly the same of what you describe, but a step in the direction, isn't it?

FOLLOW-UP

@red51: I just made a little jMonkey project to play with 3D rotation calculations and this is a summary of my findings. I hope it further explains my point of view. All values are taken from jMonkey own calculations and getters.
_____________________

1) An initial rotation of 45° around the Z object axis is expressed by:

1a) the rotation matrix
| 0.71 -0.71 0.00 |
| 0.71 0.71 0.00 |
| 0.00 0.00 1.00 |

1b) the quaternion <0.00 0.00 0.38 0.92>

1c) the 'Euler' angles 0.00X 0.00Y 0.79Z
_______________________

2) An additional rotation of 45° around the object Y axis yields:

2a) the rotation matrix:
| 0.50 -0.71 0.50 |
| 0.50 0.71 0.50 |
| -0.71 0.00 0.71 |

2b) the quaternion <-0.15 0.35 0.35 0.85>

2c) The 'Euler' angles -0.62X 0.96Y 0.52Z

It is clear that adding a second rotation around an axis does not simply add to one of the 'Euler' angles, but affects all of them.
_________________________

Just for reference, a single rotation of 45° around the object Y axis yields:

*) the rotation matrix
| 0.71 0.00 0.71 |
| 0.00 1.00 0.00 |
| -0.71 0.00 0.71 |

*) the quaternion <0.00 0.38 0.00 0.92>

*) the 'Euler' angles 0.00X 0.79Y 0.00Z

Je comprend ta déception, puisque il y a très peu de jours qui parle ma langue maternelle aussi (italien). Mais, quand même, le jeu est (relativement) nouveau, de toute façon encore dans "Early Access", la communauté est encore réduite et l'Anglais, bon gré mal gré, est la langue commune la plus répandue; peut-être un effort pour se familiariser avec va être payant, tôt ou tard...

Malheureusement, je peux écrire le français (avec quelque aide technologique!), mais je ne peux assez le parler pour expliquer ces choses, d'autant plus que je ne connais pas le vocabulaire spécifique.

Bon chance!

@red51: Thanks for the reply, I appreciate you spending time on commenting on this topic. I am not very familiar with the terminology used in game field, so I may fail to understand some detail, but I still believe there is a bug somewhere, rather than the choice of a given implementation over another.

Your description seems to imply that intrinsic rotations (i.e. relative to the reference frame being rotated, or "object coordinates") are used rather extrinsic ones (i.e. relative to the global, fixed reference frame, or "world coordinates"). I'll assume this to be true.

(Side note: as you quote three rotations around three different axes, while the "classical" Euler formalism only uses two, the first and the third rotation being around the same axis, it seems to me we are actually dealing with Tait-Bryan angles, but I'll assume them as just a variant of the Euler formalism).
______________________________

A) Euler angles should be able to represent any orientation with three appropriate elemental rotations. However, I have been unable to achieve the object orientation which can be described as:

0) the object is initially aligned with the world reference frame (grey outline)
1) rotate the object around its Z axis by, say, 45° (black outline)
2) rotate the object around its Y axis by, say, 45° (red outline)

as depicted by:

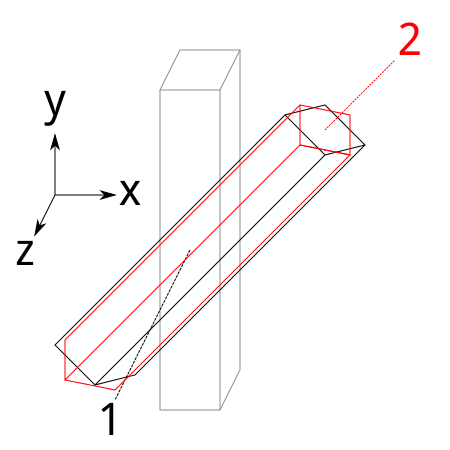
This orientation seems impossible to achieve with the current implementation. Possibly, I didn't try hard enough and I would be glad if somebody could find a way to do it, but so far this does not seem to be a complete implementation.
_____________________________

B) If intrinsic rotations are used, they should be used all over the place and, as they are "played back" in a specific order (Y - Z - X), generally different form the order in which they are created (in my example above they are created in the order Z - Y), the latter order should be converted into the former.

I'll try to explain myself elaborating on the example above.

0) Step 0 (initial rotation) can be described with the Tait-Bryan Y-Z-X angles as y = 0, z = 0, x = 0.

1) Step 1 (rotation around the object Z axis) can be described as y = 0, z = 45°, x = 0.

2) Step 2 (another, second, rotation around the object Y axis) cannot be represented as y = 45°, z = 45°, x = 0, because this represents a different final orientation in which the Y rotation is applied first, as per your description.

The actual representation of step 2 as a yaw - roll - pitch (Y-Z-X) sequence of elemental rotations should be derived by applying step 2 to step 1 obtaining a cumulative rotation matrix (or quaternion) from which to work out the individual Euler (or Tait-Bryan) angles in the chosen sequence (Y-Z-X).

I hope this might explain a bit more the issue I am facing.

This issue is flagged as fixed, but I still see it in the latest version.

Am I missing something? Really nobody else notices this issue or is affected by it?

You may start by having a look at this thread, maybe commenting on it.

Not sure to understand.

1) The import net.risingworld.api.Plugin; statement should be put before the Plugin class is used; normally, all the imports are put at the beginning of the file.

2) The Plugin class itself is in the PluginAPI.jar file; this file can be put almost anywhere as long the compiler can reach it (Java Build Path).

Usually IDE's have a way to add libraries (including our API jar) to the Java Build Path, whose details depend on the IDE itself; for instance Eclipse (the IDE I use) has it in "Project | Properties | Java Build Path | Libraries tab".

You need to import the net.risingworld.api.Plugin (and possibly several other, depending on what you do in your code) in order to use it in the code.

For what is worth, I repeated elsewhere ad nauseam my points of view, so I'll summarize them briefly:

1) I don't know if "Rising World and Monster just do not mix"; but I know that for me it would be better if they don't. Why? There is already plenty of games where fighting is a key element, adding another one would add little, if anything. I would greatly prefer a game where survival elements are provided in less abused ways, from meteo (cold, rain) to biology (hunger, ...) to anything else one can think of, possibly based on real (or realistic) elements (The Long Dark might be a good example, if only it could run better under Linux...).

And adding monsters which can be turned off would only solve half of the problem, as this alone would not add the other survival elements I hinted at.

2) I fail to understand environments in which some thing has no origin, no apparent way to survive and so on. "Monsters" usually fall in this category: what do they eat when the player is not there? Where do they come from? What do they descend from? We strive for "realistic" looking in buildings we make, we ask for better doors (just to make a silly example), for an economy, for more appropriate tools and so on and then we slip on "monsters"? I simply do not understand.

It is just my opinion of course; it is not worth more than anybody else's opinion, but neither it is worth less.

@red51 and @zfoxfire:

Eating animals: yes, I understand it is not an urgent topic. Also I do not not necessarily expect this to be implemented in a visual, 'narrative', way, with animals wandering from plant to plant and visibly eating its fruits. This would be wonderful of course, but a 'simple' availability effect, with the presence of animals in the area reducing the number of ripe fruits would already be rather useful to tune the food availability.

Growth time: well, of course, I do not mean the game should implement real growth times, with tomatoes taking 3 real time months to grow, and not even necessarily 3 game time months; I agree this would be excessive. Still, vegetables growing almost over night seems to me excessive in the other direction.

We often speak about increasing the survival aspects of RW and regularly this is intended to mean adding fictional difficulties like mobs, dungeons and so on. Removing the fictional easing elements or shot-cuts, like the two quoted above, would already go a fair length in making RW more survival oriented.

Just came back from a meeting and had not time to test try the update yet!

Quote from diegomarino80gongo

2) Can i ahve a world setting with which i select the amount of food and type of animals? there are too much harmless animals, and too few predators. and too food, of course

I vaguely remember an approximate "rule of 10" for the steps of the food pyramid: to sustain n animals in a level, at least approx. 10 x n (or more) animals are needed in the level below. E.g.: to sustain 10 carnivore animals, about 100 or more herbivore animals are needed. So, possibly RW has more predators than a real world, rather than less.

Food IS abundant indeed; still given the very low population (just 1 eater in single player; rarely more than a handful in MP) compared to the surface, it does not seem to me strikingly unrealistic. Possible points to be tuned in future could be:

a) growth of plants and trees is very quick: a real tomato plants takes about 3 months from planting the seed to ripe fruits and a real apple tree several years!

b) animals do not consume food, taking away a substantial competitor for food.

And a date for the update has been announced!

The PVP line is in the server.properties file (NOT in a permission file) and should read:

settings_pvp_enabled=false

Please pay attention to case ("false", not "False"; "..._pvp_...", not "..._PVP_...") and blanks; also be sure to edit the file with an editor which does not add any code or formatting of its own, Notepad++ is usually fine.

In most cases, the spawn point is in the area W 0 - 256, N 0 - 256 (unless you have modified it in the server.properties file), often at the W 256, N 256 point. To go there, open the console (default key is [~], I think) and type:

goto 256 256

(or any other pair of coordinates). Better to activate flying with [F2] beforehand.
I think there is also the console command

goto #spawn

but I am not sure and I cannot check it right now.

Hello PJ, welcome on board!

I also have been attracted by the friendliness of the community, as an added value to the strengths of the programme itself and I have a penchant for building elements (with an accent on landscaping too, which is nicely supported by RW and will probably improve over time).

My history has some point of contacts with yours as well as some differences, as I have worked for several years in the Microsoft Flight Simulator add-ons market (as a programmer). I also speak some basic Spanish, but my mother tongue is Italian: we can pretend to chat in Spanish, for the amusement of the real "hispano-hablantes" of the forum (there are some!).

See you!

M.

A similar experience and some details can be also found in this thread.

Quote from joni909

but it's bad that at least two of the most popular game engines (unity and unreal engine) is not for Linux users even though you can make Linux game from them

From them you can make Linux games which run under Linux, if and when they really run and often with big problems...